Authors:
(1) Oleksandr Kuznetsov, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA and Department of Political Sciences, Communication and International Relations, University of Macerata, Via Crescimbeni, 30/32, 62100 Macerata, Italy ([email protected]);
(2) Dzianis Kanonik, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA;
(3) Alex Rusnak, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA ([email protected]);
(4) Anton Yezhov, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA;
(5) Oleksandr Domin, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA.
Table of Links
1.1. The Blockchain Paradigm and the Challenge of Scalability
1.3. Our contribution and 1.4. Article structure
2. Conceptualizing the Problem
3. Our Idea for Optimizing Trees in Blockchain
4. Efficiency of adaptive Merkle trees
5. Algorithm for Merkle Tree Restructuring
6.2. Example 1.1: Binary Tree Restructuring Through Leaf Node Swapping
6.3. Example 2.1: Restructuring a Non-Binary Tree by Adding a Single Leaf
6.4. Example 2.2: Restructuring a Non-Binary Tree Through Leaf Pair Swapping
6.5. Example 2.3: Restructuring a Patricia-Merkle Tree Fragment Through Leaf Pair Swapping
7. Path Encoding in the Adaptive Merkle Tree
8.2. Technology and Advantages
9.2. Comparison with Existing Solutions
6.3. Example 2.1: Restructuring a Non-Binary Tree by Adding a Single Leaf
In this example, we explore a non-binary tree where each node can have up to four children (m = 4), closely mirroring a simplified real-world scenario of Patricia-Merkle trees in the Ethereum blockchain.
Let's assume the initial state of the tree is as shown in Figure 11.a, similar to the previous example. Also, let the newly added leaves and their probability distributions follow the pattern established in Example 1. These changes in probabilities are summarized in Table 5, which also lists the number of alternatives and the unique discrepancy value (1). Figures 21-30 depict the corresponding tree graphs.
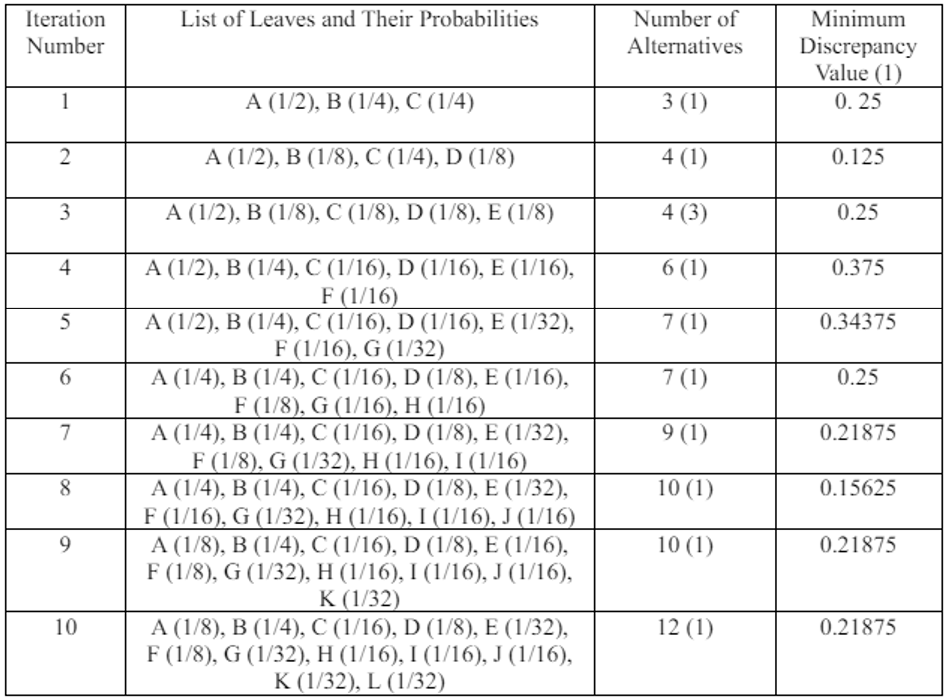
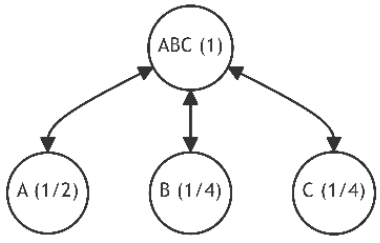
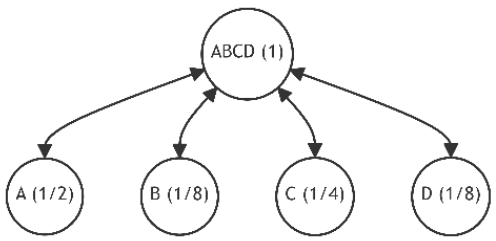
. 
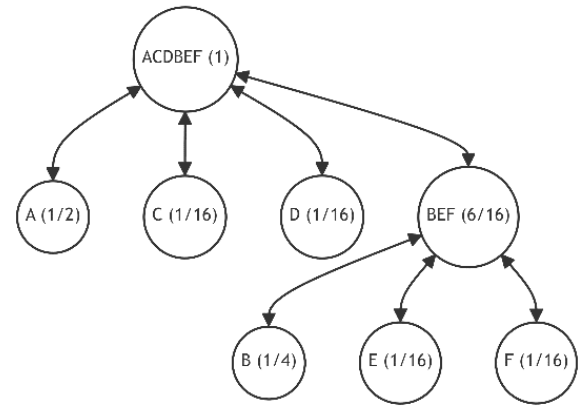
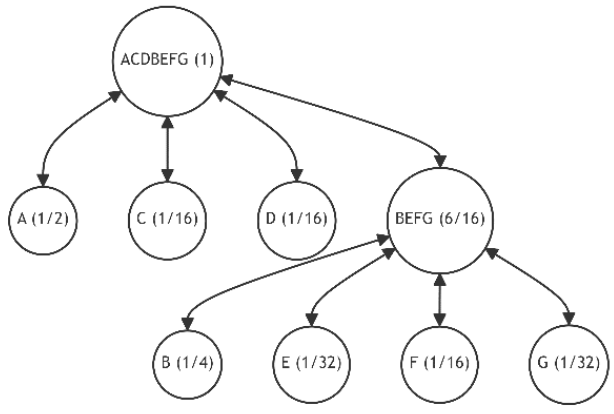
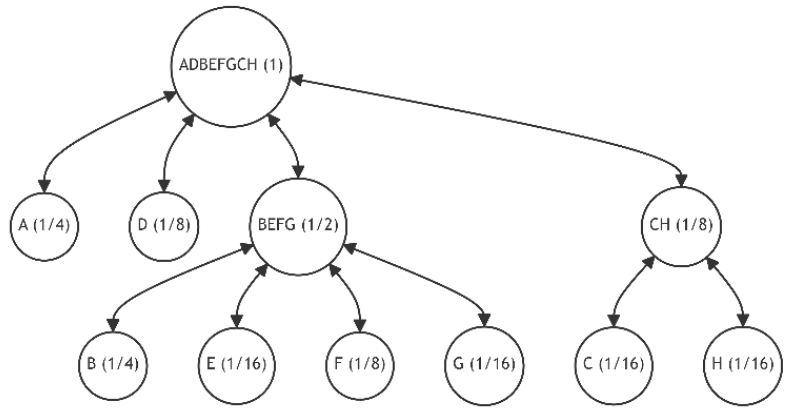
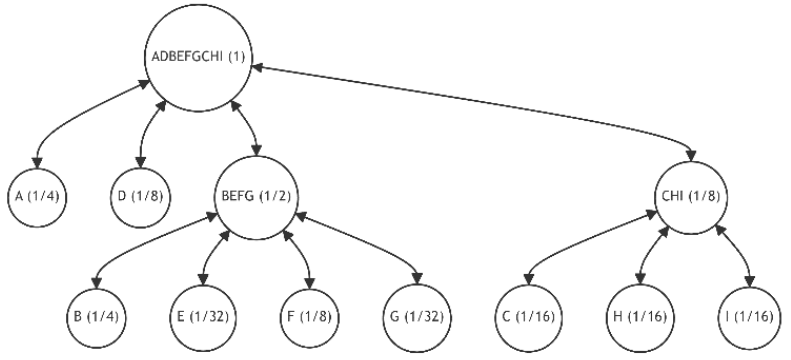
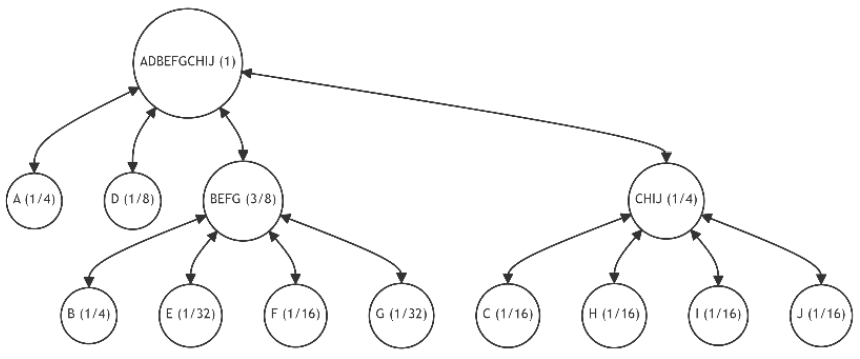
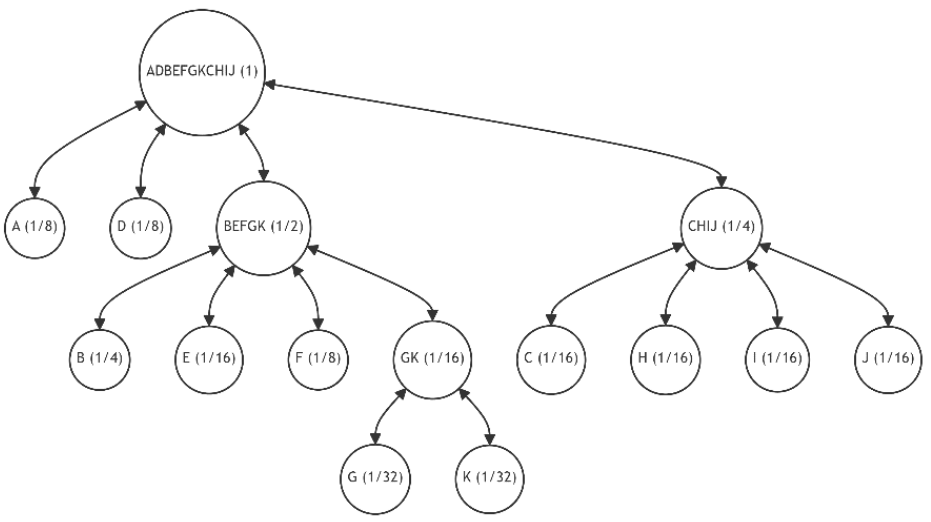
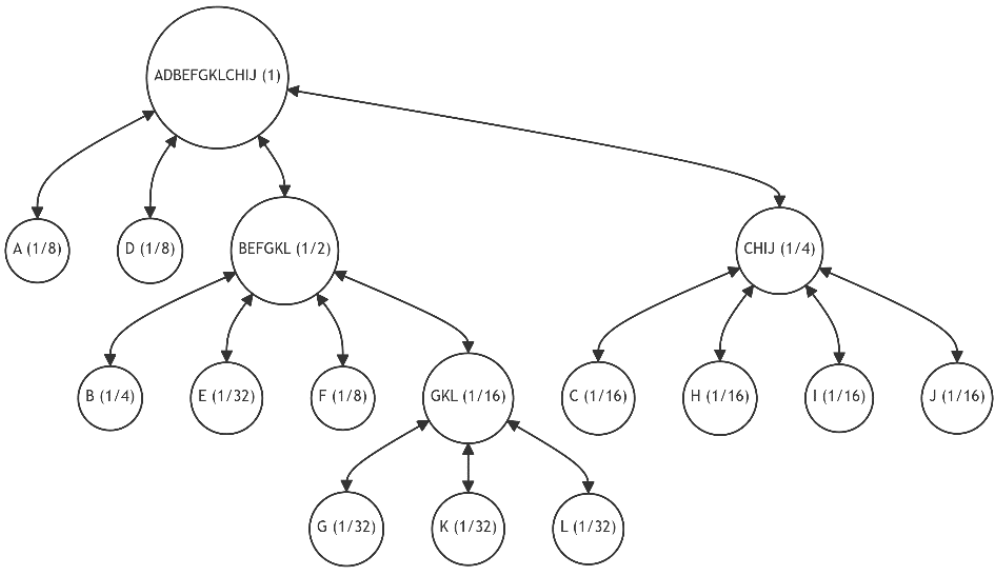
The calculations of discrepancies in Table 5 show that the configuration of the restructured trees tends towards optimality by minimizing the average path length.
Now, let's demonstrate the algorithm's operation in the mode of swapping positions between pairs of nodes, as in Example 1.1.
This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.

