Authors:
(1) Oleksandr Kuznetsov, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA and Department of Political Sciences, Communication and International Relations, University of Macerata, Via Crescimbeni, 30/32, 62100 Macerata, Italy ([email protected]);
(2) Dzianis Kanonik, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA;
(3) Alex Rusnak, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA ([email protected]);
(4) Anton Yezhov, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA;
(5) Oleksandr Domin, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA.
Table of Links
1.1. The Blockchain Paradigm and the Challenge of Scalability
1.3. Our contribution and 1.4. Article structure
2. Conceptualizing the Problem
3. Our Idea for Optimizing Trees in Blockchain
4. Efficiency of adaptive Merkle trees
5. Algorithm for Merkle Tree Restructuring
6.2. Example 1.1: Binary Tree Restructuring Through Leaf Node Swapping
6.3. Example 2.1: Restructuring a Non-Binary Tree by Adding a Single Leaf
6.4. Example 2.2: Restructuring a Non-Binary Tree Through Leaf Pair Swapping
6.5. Example 2.3: Restructuring a Patricia-Merkle Tree Fragment Through Leaf Pair Swapping
7. Path Encoding in the Adaptive Merkle Tree
8.2. Technology and Advantages
9.2. Comparison with Existing Solutions
6.4. Example 2.2: Restructuring a Non-Binary Tree Through Leaf Pair Swapping
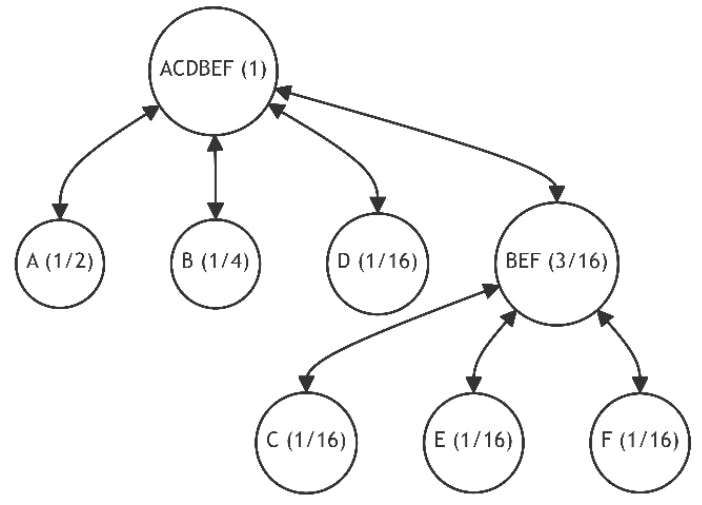
Let's delve into the most challenging scenario from Example 2, which resulted in the highest discrepancy value. This scenario corresponds to the tree graph obtained after the fourth iteration, as depicted in Figure 24. We will demonstrate how swapping the positions of leaf pairs can enhance this structure.
To form a set of alternatives for the graph in Figure 24, we observe:

Focusing on pairs with differing path lengths, we identify:

The last two alternatives are equivalent and halve the discrepancy (1), thus optimizing the final tree structure (see Figure 24.1).
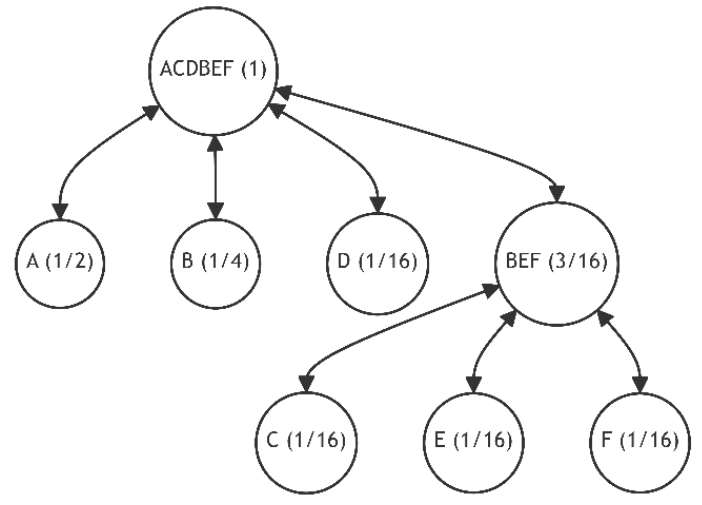
This approach allows for the dynamic restructuring of trees, minimizing the divergence between the current and optimal graph structures. By combining different rules (adding new leaves and swapping positions of existing leaves), we can achieve highly efficient structures that minimize the average path length.
Through this methodology, we underscore the algorithm's capability to swiftly adapt tree structures, ensuring an optimal configuration that aligns closely with the theoretical minimum discrepancy. This adaptability is crucial for maintaining efficient data verification processes in blockchain technologies, where the dynamic nature of transactions necessitates a flexible yet robust system for ensuring data integrity.
The proposed algorithm exemplifies a significant advancement in optimizing tree structures for blockchain applications, particularly in scenarios where non-binary trees, such as Patricia-Merkle trees used in Ethereum, are prevalent. By judiciously applying leaf swapping and addition strategies, we can significantly enhance the efficiency of these cryptographic structures, paving the way for more scalable and cost-effective blockchain operations.
In conclusion, let's explore another example of a tree with m =16 , which can be considered as restructuring a fragment of the Patricia-Merkle tree in the Ethereum blockchain.
This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.