Authors:
(1) Oleksandr Kuznetsov, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA and Department of Political Sciences, Communication and International Relations, University of Macerata, Via Crescimbeni, 30/32, 62100 Macerata, Italy ([email protected]);
(2) Dzianis Kanonik, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA;
(3) Alex Rusnak, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA ([email protected]);
(4) Anton Yezhov, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA;
(5) Oleksandr Domin, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA.
Table of Links
1.1. The Blockchain Paradigm and the Challenge of Scalability
1.3. Our contribution and 1.4. Article structure
2. Conceptualizing the Problem
3. Our Idea for Optimizing Trees in Blockchain
4. Efficiency of adaptive Merkle trees
5. Algorithm for Merkle Tree Restructuring
6.2. Example 1.1: Binary Tree Restructuring Through Leaf Node Swapping
6.3. Example 2.1: Restructuring a Non-Binary Tree by Adding a Single Leaf
6.4. Example 2.2: Restructuring a Non-Binary Tree Through Leaf Pair Swapping
6.5. Example 2.3: Restructuring a Patricia-Merkle Tree Fragment Through Leaf Pair Swapping
7. Path Encoding in the Adaptive Merkle Tree
8.2. Technology and Advantages
9.2. Comparison with Existing Solutions
6.5. Example 2.3: Restructuring a Patricia-Merkle Tree Fragment Through Leaf Pair Swapping
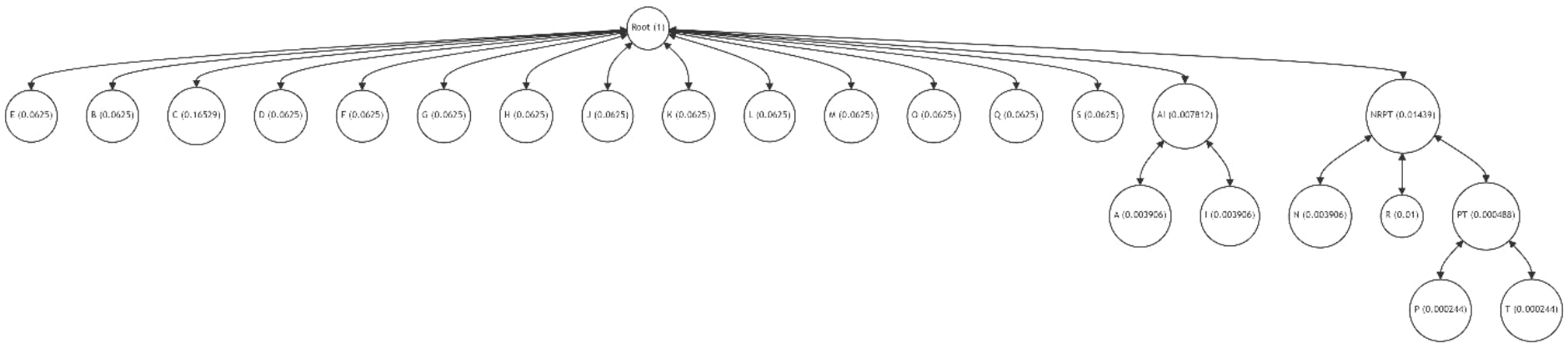
Imagine we have a fragment of the Patricia-Merkle tree with leaves (and probabilities) assigned as follows (see Figure 31):
A (0.003906), B (0.0625), C (0.16529), D (0.0625), E (0.0625), F (0.0625), G (0.0625), H (0.0625), I (0.003906), J (0.0625), K (0.0625), L (0.0625), M (0.0625), N (0.003906), O (0.0625), P (0.000244), Q (0.0625), R (0.01), S (0.0625), T (0.000244).

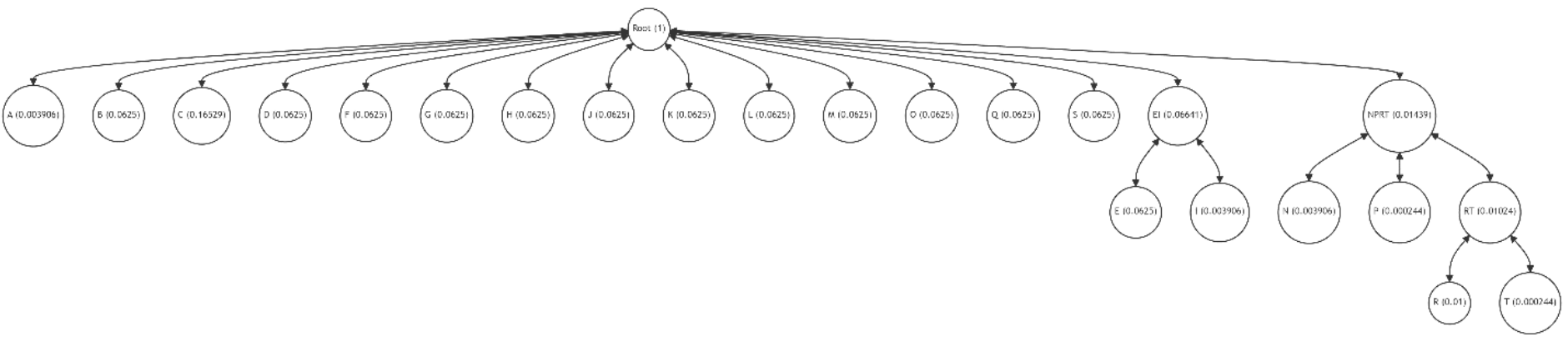
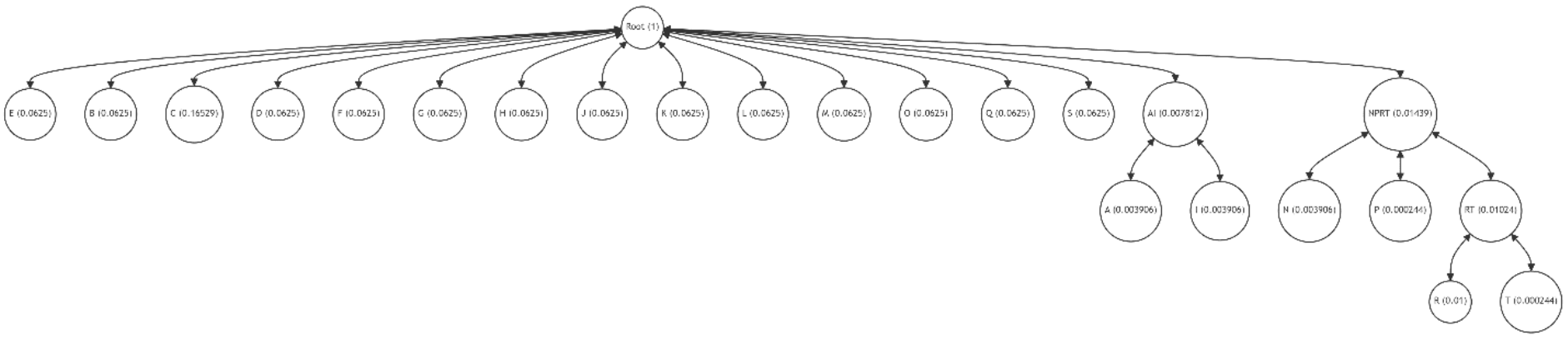
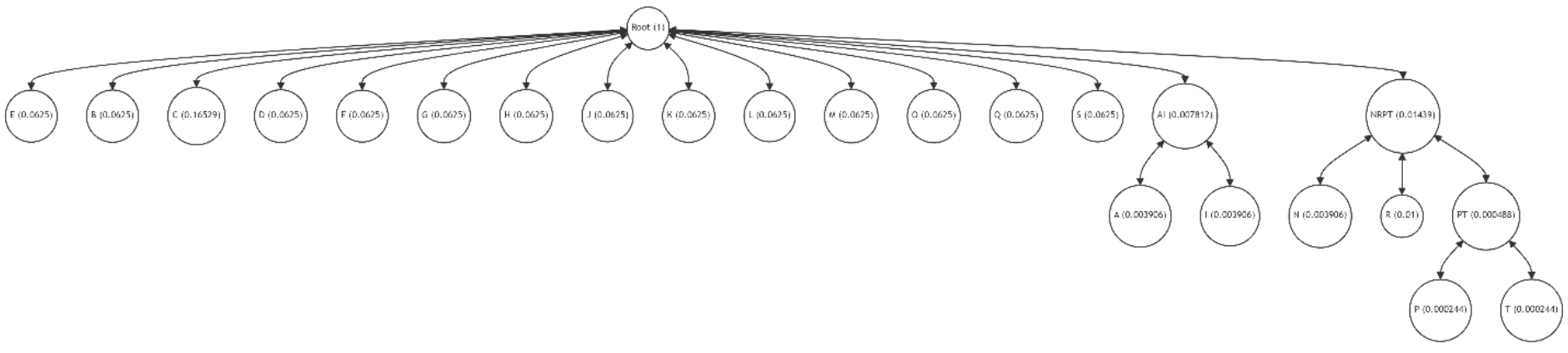
Thus, even a small number of algorithm iterations allows for a significant reduction in discrepancy (1) and optimization of the tree structure, reducing the average path length.
This example underscores the potential of our restructuring algorithm to enhance the efficiency of Patricia-Merkle trees in blockchain applications. By judiciously swapping the positions of leaf pairs, we can significantly improve the tree's structure, aligning it closer to the optimal configuration. This process not only minimizes the average path length but also contributes to the overall efficiency and scalability of blockchain operations, particularly in systems like Ethereum where Patricia-Merkle trees play a crucial role in data integrity verification.
This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.