Authors:
(1) Oleksandr Kuznetsov, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA and Department of Political Sciences, Communication and International Relations, University of Macerata, Via Crescimbeni, 30/32, 62100 Macerata, Italy ([email protected]);
(2) Dzianis Kanonik, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA;
(3) Alex Rusnak, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA ([email protected]);
(4) Anton Yezhov, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA;
(5) Oleksandr Domin, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA.
Table of Links
1.1. The Blockchain Paradigm and the Challenge of Scalability
1.3. Our contribution and 1.4. Article structure
2. Conceptualizing the Problem
3. Our Idea for Optimizing Trees in Blockchain
4. Efficiency of adaptive Merkle trees
5. Algorithm for Merkle Tree Restructuring
6.2. Example 1.1: Binary Tree Restructuring Through Leaf Node Swapping
6.3. Example 2.1: Restructuring a Non-Binary Tree by Adding a Single Leaf
6.4. Example 2.2: Restructuring a Non-Binary Tree Through Leaf Pair Swapping
6.5. Example 2.3: Restructuring a Patricia-Merkle Tree Fragment Through Leaf Pair Swapping
7. Path Encoding in the Adaptive Merkle Tree
8.2. Technology and Advantages
9.2. Comparison with Existing Solutions
3. Our Idea for Optimizing Trees in Blockchain
Figure 7 represents an innovative adaptation of the traditional Merkle Tree, incorporating principles of Shannon-Fano and Huffman statistical coding. Unlike the balanced Merkle Tree, this adaptive structure is intentionally unbalanced to optimize the verification process based on the frequency of data usage. Each leaf node (A-P) still represents a block of data with a unique hash value, but their placement in the tree now correlates with the probability of their usage.
In this adaptive Merkle Tree, the most frequently used data nodes (A, B, C, D) are positioned closer to the root, significantly shortening the path required for their verification. This strategic placement reduces the computational complexity and time required for verifying frequently accessed data. Conversely, less frequently used data nodes (M, N, O, P) are placed further from the root, reflecting their lower probability of access.
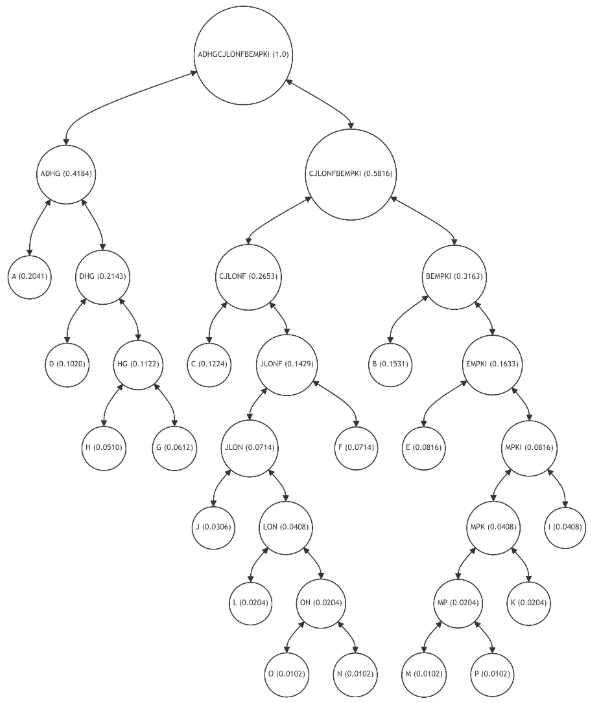
The structure of this tree is a direct application of Shannon-Fano and Huffman coding principles, where the most common elements are given shorter codes (or paths in the case of a Merkle Tree). This approach ensures that the average path length for verification is minimized, aligning the computational effort with the actual usage patterns of the data within the blockchain.
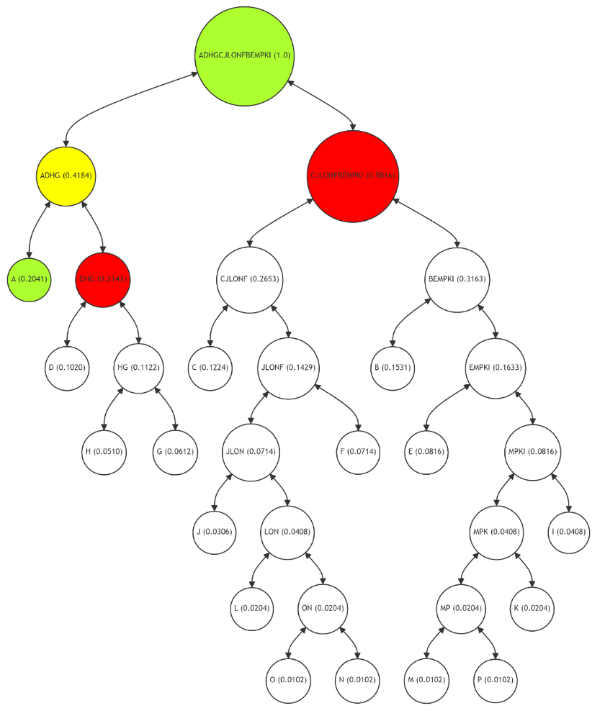
In the Figure 8, the Merkle Path for leaf node A (highlighted in green) is significantly shorter than in a balanced Merkle Tree. The path (marked in red) includes nodes DHG and CJLONFBEMPKI, with intermediate calculations (in yellow) at node ADHG. This optimized path reflects the high frequency of usage for node A, making the verification process faster and more cost-effective. The integrity of node A can be verified with fewer computational steps, demonstrating the efficiency of the adaptive Merkle Tree in handling frequently used data.
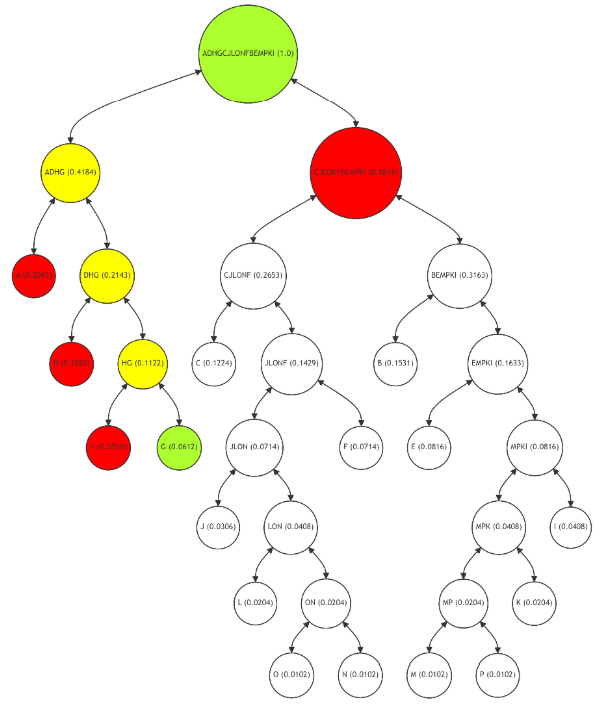
For leaf node G (Figure 9), the Merkle Path includes nodes H, D, and CJLONFBEMPKI, with intermediate calculations at nodes HG and ADHG. This path, while longer than that for node A, is still optimized based on the usage frequency of G. The adaptive tree structure ensures that the verification process remains efficient, even for nodes with moderate usage. This approach balances the need for data integrity with computational efficiency, tailoring the verification complexity to the usage pattern of each node.
The Merkle Path for leaf node P (Figure 10), a less frequently used node, is longer, including nodes M, K, I, E, B, CJLONF, and ADHG. The path reflects P's lower usage frequency, with more intermediate calculations (nodes MP, MPK, MPKI, EMPKI, BEMPKI, and CJLONFBEMPKI) required for verification. While this makes the verification process for P more resource-intensive, it is justified by the node's infrequent use. This example illustrates how the adaptive Merkle Tree allocates computational resources more efficiently, focusing on optimizing the paths for more frequently used nodes.
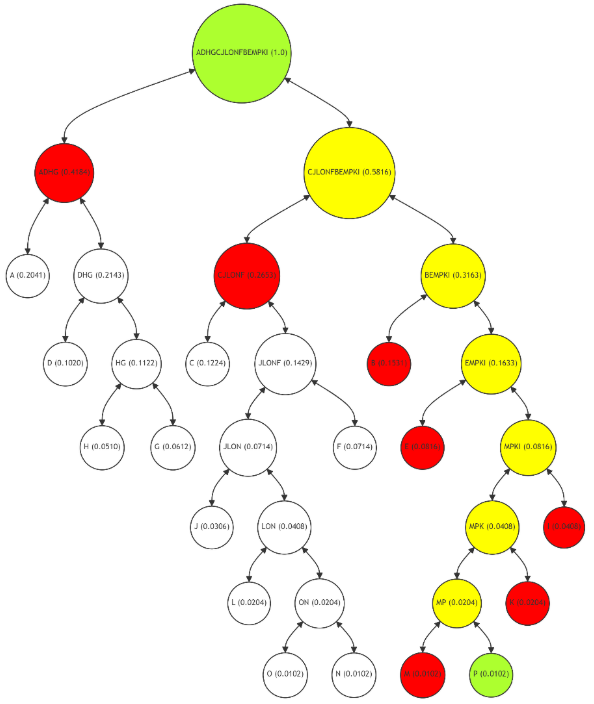
Thus, the adaptive Merkle Tree approach significantly enhances the efficiency of data verification in blockchain systems. For high-frequency nodes like A, the verification process is streamlined, requiring fewer computational steps and resources. This optimization can lead to a verification process that is up to twice as fast and cost-effective compared to a balanced Merkle Tree. Conversely, for nodes with lower usage frequencies, like P, the longer verification path is a reasonable trade-off, considering their infrequent access.
This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.

